1. 十进制和二进制的转换(掌握)

　　首先我们来学习十进制与二进制之间的转换，这是必须要掌握的哦。

　　1.1 十转二

　　如果我们想将十进制转为二进制，可以采用辗转法，将十进制除以2再取余，然后将余数和最后的1按照从下向上倒序写的方法。例如我们想将十进制的302转为对应的二进制，过程如下：

　　我们将上面每一步得到的余数和最后的1，按照从下向上倒序的方式进行编写，所以302对应的二进制数为100101110。

　　1.2 二转十

　　如果我们要把二进制转为十进制，有两种计算方法。

　　第一种计算方法，是把二进制从最高位(最左边的“1”)开始，先按照从上到下的顺序写出来。先从第1位开始计算0*2，如果每一位上对应的余数是1，在乘以”2“之后还要再加”1“，否则就加0。接着用上一次计算得到的结果乘以2，后面再加1或者是0，以此类推。壹哥给大家用下面的例子进行演示：

　　第一种计算方式其实有点复杂，我们可以采用更简单的第二种计算方法。该方法是从最低位开始，每位上的数字*2的N次幂，N从0开始记数(0、1、2......)，把每一位的乘积进行累加就是最后的结果。我们把上面的例子换成该方法进行计算，会如下所示：

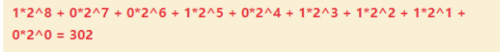
　　其实根据第2种计算方法，你可以发现规律。最低位上计算出来的十进制结果最大值就是1，往前一位的最大值是2，以此类推，4、8、16、32、64、128、256.....

　　所以如果该二进制位上是1，该位置上肯定可以得到对应的十进制最大值，否则只能得到0。比如11111111转成对应的十进制，就可以直接计算：1+2+4+8+16+32+64+128=255

　　壹哥个人推荐采用这种方式进行计算，简单快捷，基本上我们熟悉之后就可以直接口算出结果。

　　2. 二进制和八进制的转换(了解)

　　2.1 八转二

　　如果你想将八进制转为对应的二进制，可以先将八进制里的每一位一隔，然后分别将每一位换算成3位二进制的格式。比如八进制的764转成对应的二进制111110100，过程如下图所示：

　　2.2 二转八

　　如果你想将二进制转为对应的八进制，可以从低位到高位，每三位一隔，将当前三位按照(4 2 1)的方式还原成对应的1位八进制。比如我们将二进制的1100101011转成对应的八进制1453，过程如下图所示：

　　1. 二进制和十六进制的转换(了解)

　　3.1 十六转二

　　如果你想将十六进制转为对应的二进制，可以先将十六进制里的每一位一隔，然后分别将每一位换算成4位(8 4 2 1)二进制的格式。比如十六进制的a8f5转成对应的二进制1010 1000 1111 0101，过程如下图所示：

　　3.2 二转十六

　　如果你想将二进制转为对应的十六进制，可以从低位到高位，每四位一隔，将当前四位按照(8 4 2 1)的方式还原成对应的1位十六进制。比如我们将二进制的11 1010 0010 1010转成对应的十六进制3a2a，过程如下图所示：

　　1. 负数的二进制(了解)

　　不仅正数可以有对应的二进制，负数也有对应的二进制。在计算机中，任何数据都是以补码的形式进行存储的。正数的原码、补码和反码都完全一样。但是负数的原码、反码、补码却不一样：

　　负数的原码=将正数的原码符号位(最高位)改为1;

　　负数的反码=符号位不变，其他位取反;

　　负数的补码=负数的反码+1。

　　壹哥在之前的文章中讲过，计算机中，最高位表示符号位，0表示正数，1表示负数。接下来壹哥就以-24和-68为例，给大家讲一下负数的二进制转换。

　　4.1 负数转为二进制

　　根据前面的内容，我们可以计算出正数24的原码是00011000(反码、补码也是这个)。所以-24对应的原码就出来了，我们直接将00011000的最高位改成1就行了，即-24的原码是10011000。于是，-24的反码也出来了，最高位不变，其余位全部取反，反码就是11100111。而-24的补码则是反码+1，所以-24的补码=11101000。如下图所示：

　　4.2 二进制转为负数

　　既然我们可以将负数转为对应的二进制，当然也可以逆运算。假如我们现在有个二进制，补码是10111100(高位是I表示负数)，我们要按照负数转二进制的逆运算进行操作。先计算出该补码对应的反码，反码=补码-1，即反码=10111100-1=10111011。接着根据反码计算出原码，原码=符号位不变，其他位取反=11000100。所以最终对应的十进制数是-68。

　　1. 小数的二进制(了解)

　　另外小数和二进制之间也可以实现转换。

　　5.1 小数转二进制

　　12.02 0.02*2=0.04

　　如果我们想将小数转为对应的二进制，整数和小数是分开计算的。如果有整数，则把整数单独转为对应的二进制。小数部分的计算则相对麻烦，主要是小数部分乘以2，取整数部分依次从左往右放在小数点后，直至小数点后为0。例如小数0.125的具体转换过程如下：

　　1.将小数部分0.125乘以2，得0.25，取整数部分0记录下来;

　　2.再将小数0.25乘以2，得0.5，再取整数部分0记录下来;

　　3.再将小数部分0.5乘以2，得到整数1.0，再取整数部分1记录下来。因为1.0的小数点后为零，结束乘2的循环过程。

　　最终我们得到0.125对应的二进制结果0.001，如下图所示：

　　5.2 二进制转小数

　　如果我们想将二进制转为对应的小数，可以从小数点以后开始，依次将当前位数上的数字乘以2的-1到-N次方，再累加。比如我们想将0.0101转为对应的小数，则是02-1+12-2+02-3+12-4=0.3125。如果你口算不出来结果，可以用计算器哦。

　　至此，就把计算机中的进制问题给大家讲解完毕了。现在你对进制转换都掌握了吗?其实今天的内容，与Java没有太大关系，所有关于编程开发或计算机技术相关的学习，都应该有进制的基础。所以学习完今天的内容之后，对我们加深理解计算机的底层也是很有帮助的哦。